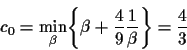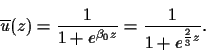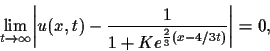Next: Discretization: Fixed Domain with Up: Adaptive Moving Mesh Solution Previous: Adaptive Moving Mesh Solution
We consider the Nagumo reaction-diffusion equation
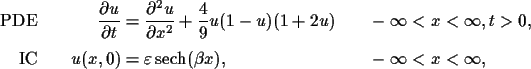
The initial condition parameter 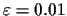 is chosen to give a small globalized perturbation to
the unstable steady state solution u=0.For any
is chosen to give a small globalized perturbation to
the unstable steady state solution u=0.For any
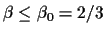 , the initial condition will evolve into a monostable
travelling wave solution, i.e., we have
, the initial condition will evolve into a monostable
travelling wave solution, i.e., we have
with
the monostable wavespeed relationship between the constant travelling wave velocity
c and the initial condition parameter 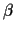 .
.
If we set 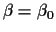 then we will observe evolution to a wave of minimum
wavespeed
then we will observe evolution to a wave of minimum
wavespeed
Any travelling wave solution takes the form
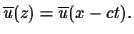 For the Nagumo PDE it follows that
For the Nagumo PDE it follows that
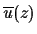 must satisfy the ordinary differential equation
must satisfy the ordinary differential equation
is satisfied. For 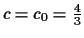 we have the exact travelling wave solution
we have the exact travelling wave solution
Now the initial condition and this minimum speed travelling wave have the same
asymptotic behaviour as 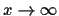 , i.e.,
, i.e.,
This is sufficient to ensure that the IC will evolve to the exact
travelling wave solution under time integration. That is,
when 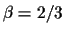 .
.



Next: Discretization: Fixed Domain with Up: Adaptive Moving Mesh Solution Previous: Adaptive Moving Mesh Solution
Michael Lunney
2000-08-04
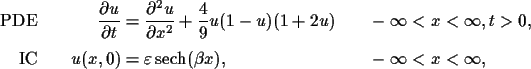
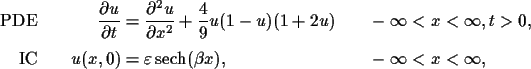
![]() is chosen to give a small globalized perturbation to
the unstable steady state solution u=0.For any
is chosen to give a small globalized perturbation to
the unstable steady state solution u=0.For any
![]() , the initial condition will evolve into a monostable
travelling wave solution, i.e., we have
, the initial condition will evolve into a monostable
travelling wave solution, i.e., we have ![]() then we will observe evolution to a wave of minimum
wavespeed
then we will observe evolution to a wave of minimum
wavespeed