This problem investigates the concept of a derivative from the geometric perspective of limiting secant lines going to a tangent line. It also allows you to explore the rules of differentiation using Maple.

a. Consider the function

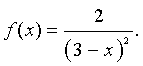
We want to investigate the derivative of f(x) at x = 2 by observing secant lines that pass through the points (2, f(2)) and (2 + h, f(2 + h)) for different values of h. The slope of the secant line is given by

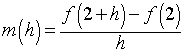
and this line always passes through the point (2, f(2)). Find the equations of the 4 secant lines (in slope-intercept form) using h = 0.5, 0.2, 0.1, and 0.05. Use Excel to graph f(x) and the 4 secant lines for x in the interval [1, 2.95]. Limit the range, so that y is in the interval [-10, 20].

b. Find the general formula for the slope of the secant line through x = 2 and x = 2 + h. The slope of the tangent line is found by taking the slope of the secant line and letting h tend toward zero. This becomes the derivative of f(x) at x = 2. Find the derivative of f(x), f '(x), at x = 2. Find the equation of the tangent line at x = 2, then use Maple graph f(x) and the tangent line for x in the interval [0,3]. (Use the same limits on the range as in Part a.).
Plot a second graph in Maple for both, f(x) and the tangent line, for a smaller interval about the point of tangency, choose [2-0.2,2+0.2]. Repeat this zooming process for an even tighter interval [2-0.02,2+0.02]. What can you conclude from this process? Explain. (Note that you must include 3 graphs for this part and you must choose your y ranges appropriately [i.e. tight around the graph of the functions]).

c. Differentiate the following functions using Maple. You are just about to learn a collection of differentiation rules, so you should be looking for patterns to help you in the future as we learn more about derivatives.