Math 121 Calculus for Biology
Spring Semester, 2007
Lab Help
26-Apr-07
|
Math 121 Calculus for Biology |
26-Apr-07 | |
|---|---|---|
|
|
|
|
This lab begins with a graphing and
derivative problem for which Maple should help.
The second problem teaches you how to use the command
Solver in Excel
to fit any arbitrary function (with any number of parameters) to
some data.
Question 1: Graphing a polynomial times an exponential (K1).
This problem extends the work that we are doing in class
on finding minima and maxima of a function to a more complicated function. You
will also find points of inflection. You will want to use Maple to differentiate
this function and find values of the extrema. Maple will help to find the points
of inflection by taking the second derivative. The Maple commands that you need
are listed below (and you may want to review previous help sheets). First, define
the function.
> f : = x -> (16-x^2)*exp(-x^2);
Next you should plot the function on the intervals listed to have an idea of what you are examining.
> plot(f(x), x = -10..10);
To find the derivative you type:
> df := diff(f(x), x);
You can simplify the expression by typing either of the following commands.
> simplify(%); factor(%);
To graph the derivative you type
> plot(df, x = -10..10);
To find when the derivative is zero, you first look on the graph to get an approximate idea. Then you type
> xc := fsolve(df = 0, x = 1..10); f(xc);
This second command gives the function value of the maximum or minimum.To find a point of inflection we take the second derivative, simplify it, then set it equal to zero. Finally, we do a function evaluation at the point of inflection.
> sdf := diff(df, x); factor(%);
> xpoi := fsolve(sdf = 0, x = 1..10); f(xpoi);
Question 2: Continuous Yeast Growth (L2).
This lab examines a yeast culture that begins in exponential
growth phase and continues until reaching stationary growth. We use Excel
to determine the growth parameters for logistic growth of the yeast culture,
identifying several of the key elements of this growth curve with techniques
from Calculus.
You begin the problem by copying the data from the lab to an Excel
spreadsheet with Time in Column A and Volume
(population) in Column B. These data can be graphed
(as data points) to see the growth of the culture. In Column
C we want to put our logistic growth model given by the formula
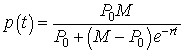
and compare this Predicted Volume to the observed values. To make the formula for P(t) convenient to implement we can make named variables in Excel. Type the labels "P0", "M" and "r" into cells F1 through F3, and select the cells F1:G3. With these six cells selected, pull down the Insert menu and choose Names:Create. The dialog box that pops up should have the "create names in left column" box checked. Say OK. The contents of cells G1:G3 now represent the named variables and will show up as such in formulas. We make initial guesses at the growth parameters. Begin with P0 = 1, and place this in G1, then proceed to guess M to be the largest value observed for the volume in the data and place this in G2. As a rough guess, let r = 0.1 and place this in G3. From the formula above, we insert the equation for the model in C2 (with the assumption that Row 1 contains labels for the different columns). Since we want the equation to use our model parameters, from the formula we write the model as
When we fill down, named parameter value continue to refer to the same cell rather than shifting. Next you fill down the model to the end of the data.
In Column D, you compute the square error between the model and the data (= (C2-B2)^2). In the cell below the last square error computation, click on the S symbol on the toolbar to sum the square error between the data and the model. This is the quantity we want to minimize.
To find the least sum of square errors, we use Excel's Solver. This should be a choice under the Tools menu, but the first time it is used it has to be installed by choosing Add-ins from the Tools menu. Highlight the cell with the sum of square errors, then click on Solver under the Tools menu. A window will pop up with the Target Cell being the one you just selected. You will need to check that you want to minimize this Target Cell, then click in the window for By Changing Cells and highlighting the cells G1:G3, which contain our model parameters. Finally, click on the Solve button, and Excel will automatically adjust your model parameters to minimize the sum of the squares of the errors. You should see the sum of square errors drop and the values for P0, M, and r change. This gives you your best model through the data.
The last step for Part a is to graph the model. In Column I, you put time, t, for the model (starting with t = 0), while Column J will have the equation for the model using the parameters in G1:G3 and the time from Column I. You increment the time to make sure that your graph has about 30-60 data points evenly spaced. (For example, if your data goes to 35 hours, then you might increment by one hour, so if I2 has t = 0, then take I3 to have = I2+1.) Fill down in Column J, then add this model to your graph.
Parts b and c follow from the techniques you have learned in class and Lab. You may want to use Maple to help with the differentiation. Make your plots using Excel.