Waves and Patterns in Nonlinear Systems - Summer 2015

AARMS-PIMS Summer School in
Differential Equations and Numerical Analysis
July 6 - 31st, 2015, Dalhousie University, Halifax

http://mathstat.dal.ca/~tkolokol/summer/

 

Instructors: Prof. Ricardo Carretero (rcarretero@mail.sdsu.edu)
Prof. Andrea Bertozzi (bertozzi@math.ucla.edu)
TA: Julia Rossi (julia.rossi@gmail.com)
Lectures:
Lectures: Mo-Fr: 10:30-12:00 @ DUNN-117
CompLab: Mo-Fr: 5:30-6:30 @ DUNN-301

Description:

The study of nonlinear systems has quietly and steadily revolutionized the realm of science over recent years. It is known that for nonlinear systems new structures emerge that have their features and peculiar ways of interacting. Examples of such structures abound in nature and include: vortices (like tornadoes or eddies in water tanks), solitons (bits of information used in optical fiber communications, water waves, tsunamis, humps of coherent matter waves, etc, ...), spirals (biological aggregates and chemical reactions). This course is intended as an introduction to the theory of Nonlinear Waves and their applications. The course is intended for senior undergraduate and graduate students in Applied Mathematics, Computational Science, Engineering, Physics, Chemistry, Biology, etc. Examples from interdisciplinary areas will be covered. Most of the concepts and examples will be supplemented with Matlab-based codes. As part of the course, students will be given access to a computer laboratory to complete the computerbased coursework.

 

Two colliding solitons of the shallow-wave nonlinear equation. As it is clear from picture the superposition of the waves is not valid and the waves behave more like two particles that collide elastically.


Reference Material:

You do not need to buy any book(s) as I will be distributing a set of notes for the course.
  • Solitons: an Introduction. P.G. Drazin and R.S. Johnson, Publisher: Cambridge University Press.

  • [Nonlinear Partial Differential Equations.
    L. Debnath, 2nd Ed., Birkhäuser 2005.]

  • Additional material will be drawn from several reference books and journal articles.

  • A set of (rough) notes will be distributed.

 
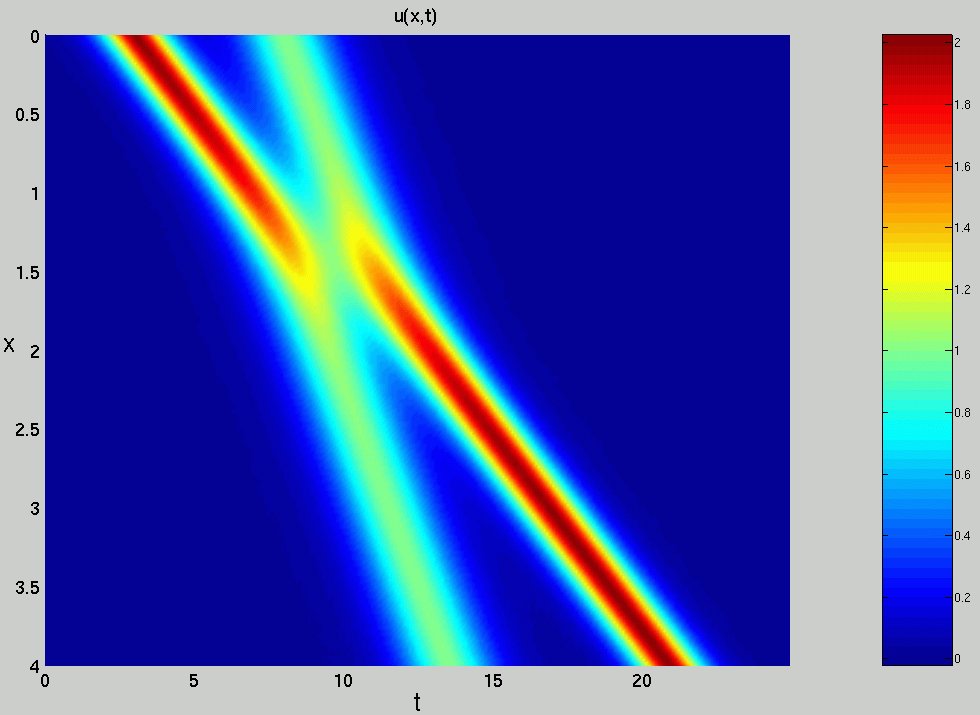
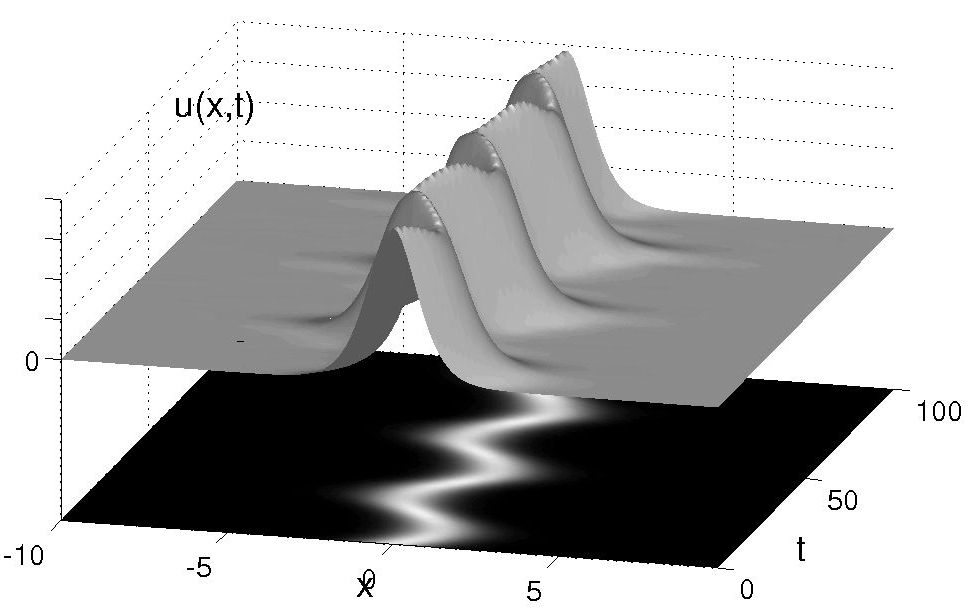
Soliton of condensed matter (Bose- Einstein condensate) trapped in a magnetic trap. The soliton behaves like a quasi-particle that oscillates left-to-right following harmonic oscillations described by Newton s Second Law of motion.