In a moving frame of reference, we truncate the infinite spatial domain
![]() to
to
![]() and set
and set
A Neumann boundary condition
A Robin boundary condition
|
Using the method of lines with Hermite collocation for the spatial discretization
we numerically integrate the Nagumo initial-boundary value problem in the speed
c0=4/3 moving frame of reference. A uniform moving spatial
mesh with N=80 nodes and
![]() is used, to facilitate
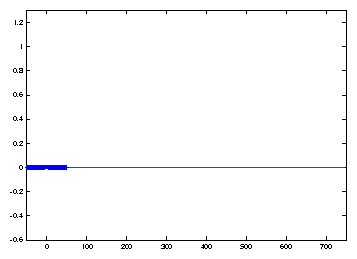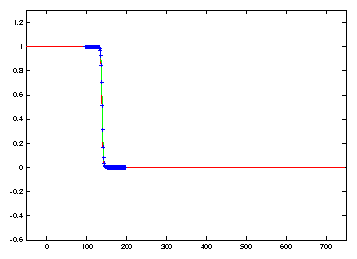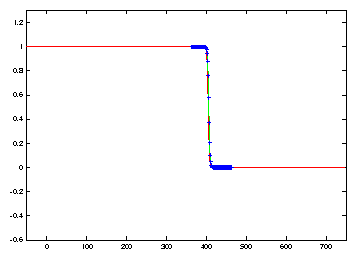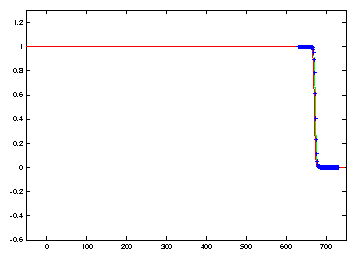
comparison with the fixed domain results. Figure 2
shows that the discrete (blue) solution closely approximates the the exact solution
(in red) to the Nagumo travelling wave initial value problem.
is used, to facilitate
comparison with the fixed domain results. Figure 2
shows that the discrete (blue) solution closely approximates the the exact solution
(in red) to the Nagumo travelling wave initial value problem.
The advantage of the moving frame of reference over the fixed frame of reference
is that using a smaller computational domain allows a smaller spatial discretization
step size ![]() to be used, which gives a closer approximation2 to the continuous problem. If the
wavespeed and decay rate parameters c0 and
to be used, which gives a closer approximation2 to the continuous problem. If the
wavespeed and decay rate parameters c0 and ![]() are not known a priori, this close relationship between
the continuous and discrete problem can be used to compute numerical approximations
for these parameters.
are not known a priori, this close relationship between
the continuous and discrete problem can be used to compute numerical approximations
for these parameters.