The resulting initial boundary-value problem for the Nagumo equation is discretized
using a method of lines approach based on a cubic Hermite collocation method
on a uniform spatial grid ![]() for
for ![]() . For large N (e.g., N=800) the solution
to the truncated initial-boundary value problem closely approximates the Nagumo
initial-value problem solution over a long time range
. For large N (e.g., N=800) the solution
to the truncated initial-boundary value problem closely approximates the Nagumo
initial-value problem solution over a long time range
![]() Note that 525 is the approximate number of time units
required for a wavefront of speed c=4/3 to advance 700 spatial units
towards the right boundary. Note that the approximation of this travelling wave
evolution problem over an arbitrarily long time interval becomes prohibitively
expensive because for the size of the fixed frame of reference
Note that 525 is the approximate number of time units
required for a wavefront of speed c=4/3 to advance 700 spatial units
towards the right boundary. Note that the approximation of this travelling wave
evolution problem over an arbitrarily long time interval becomes prohibitively
expensive because for the size of the fixed frame of reference
![]() must be increased if the wavefront location
is to remain in the computational spatial domain.
must be increased if the wavefront location
is to remain in the computational spatial domain.
Unfortunately, as the spatial domain size is increased, the number of mesh
points N must be increased. If N is too small relative to the
domain length ![]() , then over long time intervals, discretization
errors cause the wavefront to propagate too quickly. For example, with N=80
and
, then over long time intervals, discretization
errors cause the wavefront to propagate too quickly. For example, with N=80
and ![]() discretization results in a wavefront which propagates at
a constant speed which is 20 per cent faster than the exact travelling wave
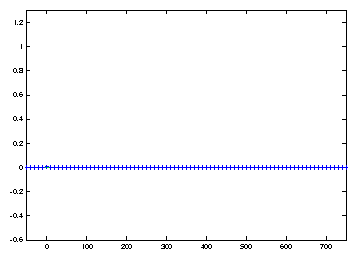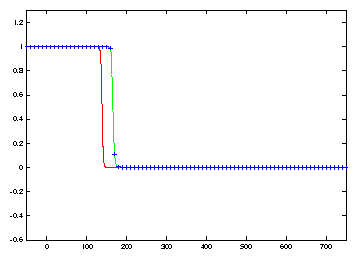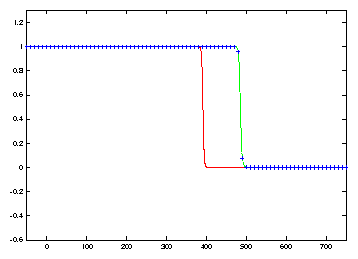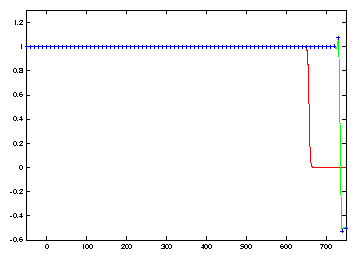
solution. See Figure 1. The first
twelve frames illustrate how the growth of propagation errors which result when
a coarse mesh is used. Ultimately the coarse discretization results in an oscillation
which produces a spurious asymptotic state connecting the two stable steady
solutions u=1 and u=-1/2.
discretization results in a wavefront which propagates at
a constant speed which is 20 per cent faster than the exact travelling wave
solution. See Figure 1. The first
twelve frames illustrate how the growth of propagation errors which result when
a coarse mesh is used. Ultimately the coarse discretization results in an oscillation
which produces a spurious asymptotic state connecting the two stable steady
solutions u=1 and u=-1/2.
|
If adaptive methods are applied to this problem, a natural choice of mesh
is one which places more points in regions where the solution is changing, i.e.,
along the wavefront connecting the u=1 and u=0 states. Also it
is important to place points in regions where the solution is unstable, i.e.,
where ![]() . In terms of equidistribution with monitor functions, [Li et al., 1999] reported
poor results with the arclength monitor function (applied to the Fisher equation).
Better results with adaptive equidistribution on a fixed mesh can be obtained,
but only by using non-standard monitor functions, such as the curvature monitor
function
. In terms of equidistribution with monitor functions, [Li et al., 1999] reported
poor results with the arclength monitor function (applied to the Fisher equation).
Better results with adaptive equidistribution on a fixed mesh can be obtained,
but only by using non-standard monitor functions, such as the curvature monitor
function
![\begin{align*}M(u,u_{xx}) = \sqrt{1 + [ 1.5(1-u) ]^2 +
\biggl[ 1000(1.015-u) \frac{\partial^2 u}{\partial x^2} \biggr]^2}
\end{align*}](img49.gif)
weighted to favour points where ![]() which was defined by [Qiu & Sloan, 1998].
which was defined by [Qiu & Sloan, 1998].
However, the numerical approximation of travelling wave evolution over long time intervals is better accomplished with a moving coordinate system, which we consider in the following section: