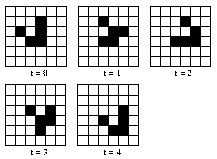Lectures:
In this page we'll post useful information about the lectures: source codes,
data, references, etc...
Go straight to bottom: BOTTOM
Matlab:
Maple:
Bibliographic material:
- Spatio-temporal
Pattern Formation, with examples from Physics, Chemistry, and Material Science.
D. Walgraef, Springer 1996.
- Phillip Ball's "The Self-made Tapestry : Pattern Formation in Nature":
Electronic
book. Access for SDSU only.
Phillip Ball's color plates
- Computation in Cellular Automata: A Selected Review
Melanie Mitchell
In T. Gramss, S. Bornholdt, M. Gross, M. Mitchell, and T. Pellizzari, Nonstandard
Computation, pp. 95-140. Weinheim: VCH Verlagsgesellschaft, 1998. SFI
Working Paper 96-09-074
- A New Kind of Science,
S. Wolfram, Wolfram Media, Champaign, IL, 2002.
- Pattern formation
outside of equilibrium
M.C. Cross and P.C. Hohenberg
Reviews of Modern Physics, 65 (1993) 851-1112.
PDFs in 40 pages chunks:
p001-040, p041-080,
p081-120,
p121-160,
p161-200,
p201-240,
p241-273.
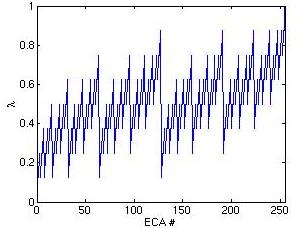
- Christopher Langton's:
- Life at the edge of chaos.
In : C.G. Langton, J.D. Farmer, S. Rasmussen and C. Taylor (eds.)
Artificial Life II: Santa Fe Institute Studies in the Sciences of Complexity
. Vol. 10.
Reading, MA: Addison-Wesely, pp. 41-91, 1991.
- Computation at the edge of chaos, Physica D, 42, 12-37
(1990).
- Chaos:
An Introduction to Dynamical Systems.
Authors: Kathleen T. Alligood, Tim D. Sauer, James A. Yorke. Publisher: Springer
1996.
Lab:
GMCS-422 computer labs: Weekly
Schedule
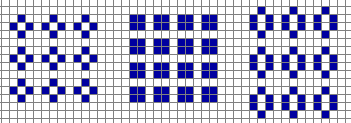
Introduction:
Cellular Automata:
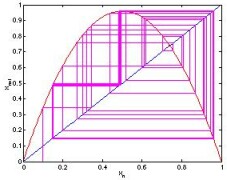
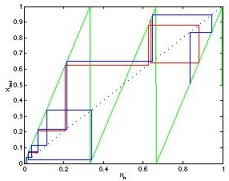
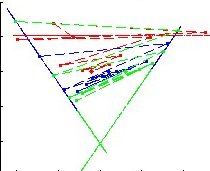
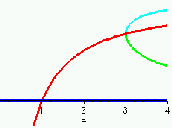
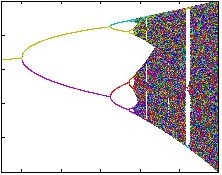
Maps:
Differential equations:
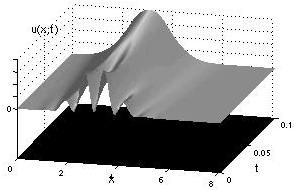
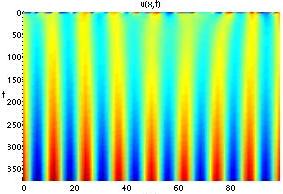
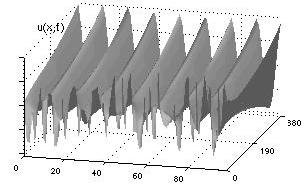
Pattern formation in one-species 1D reaction
diffusion system:
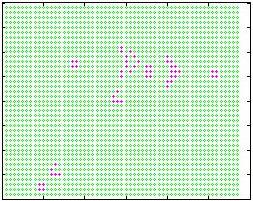
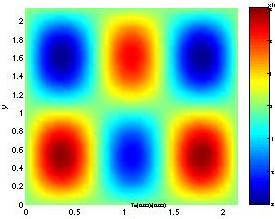
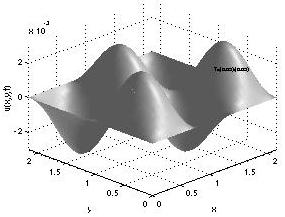
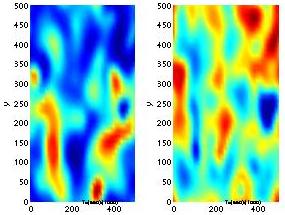
Pattern formation in one-species 2D reaction
diffusion system:
Pattern formation in two-species 1D reaction
diffusion system:
Pattern formation in two-species 2D reaction
diffusion system:
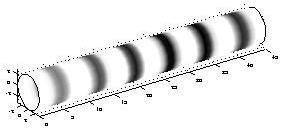
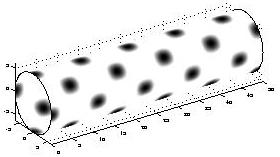
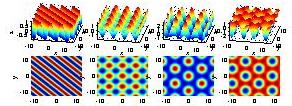
How the leopard got its spots?
- Modes for a cylindrical domain: tail.m.

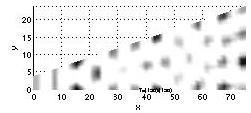
- PDE reaction diffusion equation model for pattern formation of spots/stripesw
in the coat on embyonic mammals:
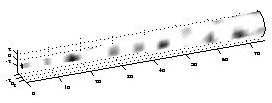
- Conic tail geometry:
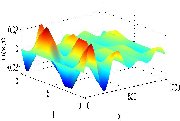
Pattern formation in two-species 2D system
(Lotka-Volterra):
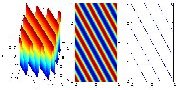
Plane waves:
Mechanical oscillations in a bridge: