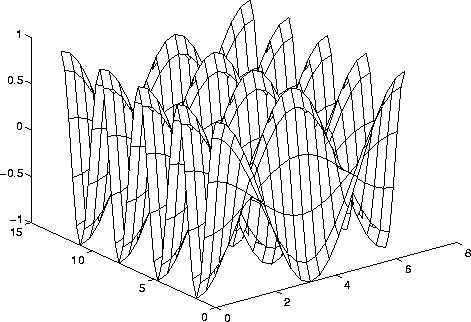
Figure 8: Using the mesh command
In order to create a graph of a surface in 3-space (or a contour plot of a surface), it is necessary to evaluate the function on a regular rectangular grid. This can be done using the meshgrid command. First, create 1D vectors describing the grids in the x- and y-directions:
>> x = (0:2*pi/20:2*pi)'; >> y = (0:4*pi/40:4*pi)';Next, ``spread'' these grids into two dimensions using meshgrid:
>> [X,Y] = meshgrid(x,y); >> whos Name Size Bytes Class X 41x21 6888 double array Y 41x21 6888 double array x 21x1 168 double array y 41x1 328 double array Grand total is 1784 elements using 14272 bytesThe effect of meshgrid is to create a vector X with the x-grid along each row, and a vector Y with the y-grid along each column. Then, using vectorized functions and/or operators, it is easy to evaluate a function z = f(x,y) of two variables on the rectangular grid:
>> z = cos(X).*cos(2*Y);
Having created the matrix containing the samples of the function, the surface can be graphed using either the mesh or the surf commands (see Figures 8 and 9, respectively):
>> mesh(x,y,z) >> surf(x,y,z)

Figure 8: Using the mesh command
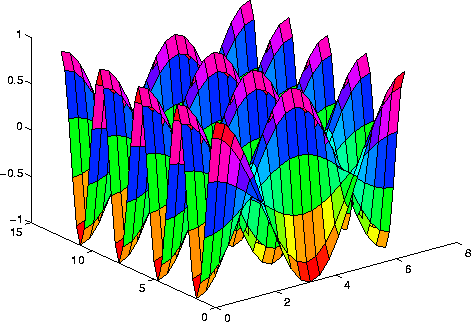
Figure 9: Using the surf command
(The difference is that surf shades the surface, while mesh does not.) In addition, a contour plot can be created (see Figure 10):
>> contour(x,y,z)
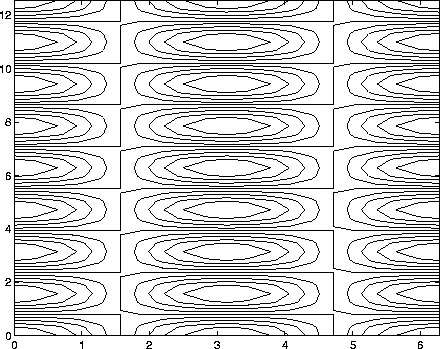
Figure 10: Using the contour command
Use the help command to learn the additional options. These commands can be very time-consuming if the grid is fine.