


Next: BLOW-UP (May 31, 2000) Up: Chemotaxis: blow up and Previous: Chemotaxis: blow up and
The equations for chemotaxis that we are using are given by [1]
![\begin{displaymath}
\begin{array}{rcl}
u_t &=& d_1 \nabla^2 u - \chi \nabla(u\na...
...\ [2.0ex]
v_t &=& d_2 \nabla^2 v - \mu v + \beta u,
\end{array}\end{displaymath}](img1.gif) |
(1) |
where u(x,t) is the population and v(x,t)
is the concentration of chemotactical substrate. The parameters d1
and d2 are the diffusion constants for u and v
respectively, 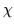 is the chemotactic parameter,
is the chemotactic parameter, 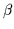 is the production rate of chemotactic substrate by the population
and
is the production rate of chemotactic substrate by the population
and 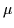 is the death or decay rate of the chemotactic substrate. In one
dimension the model reads
is the death or decay rate of the chemotactic substrate. In one
dimension the model reads
![\begin{displaymath}
\begin{array}{rcl}
u_t &=& d_1 u_{xx} - \chi (u v_x)_x \\ [2.0ex]
v_t &=& d_2 v_{xx} - \mu v + \beta u.
\end{array}\end{displaymath}](img5.gif) |
(2) |
Figure:
Traveling peak due to non-symmetry of the domain
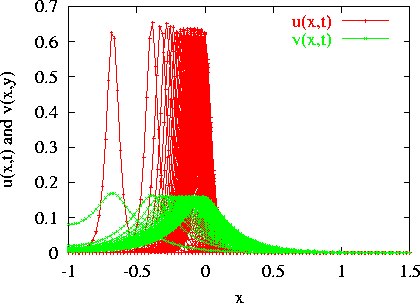 |
When starting with an initial peak symmetric w.r.t. the center of the
domain, the stationary solution is reached and it stays put at the center of
the domain. However, if we start with an initial peak centered at a different
point, it starts to travel towards the boundary. The velocity of the peak increases
as it gets closer to the boundary, see figure 1.
Figure:
Position of the peak as a function of time t for
d1=d2 ranging from 0.01 to 0.05 (right to left).
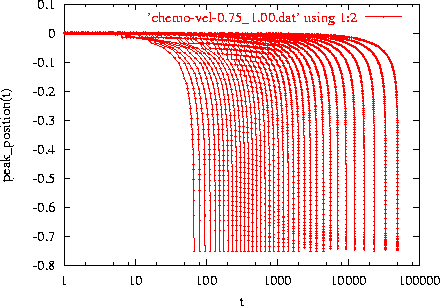 |
A typical plot for the position of the peak as time evolves in given in figure
2. In the figure we plot the trajectory
of the peak for increasing diffusion parameter d1=d2
corresponding to plots from right to left.
Figure:
Height of the peak as a function of time t for
d1=d2 ranging from 0.01 to 0.05 (top to bottom).
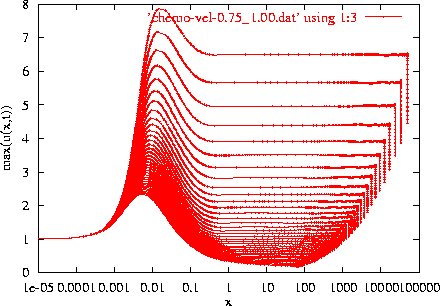 |
The height of the peak also shows interesting behaviour. As it can be seen
in figure 3 the height of the peaks first
grows and then decays to the stationary shape. After that it travels without
changing its shape until it hits the boundary and its height is affected (right-most
part of the curves).
Figure:
Escape time as a function of the diffusion
d1=d2
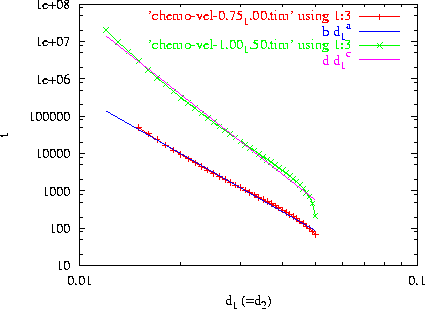 |
In order to check for metastability we want to measure the time it takes for
the peak to hit the boundary as a function of the diffusion. This elapsed time
te, referred from now on as escape time, is
depicted in figure 4 as a function of
d1=d2 in a log-log plot for two different
sizes of the domain. From the figure we can observe that the escape time behaves
closely as:
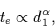 |
(3) |
for negative 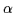 . The deviations from the straight fit (see lines in figure 4)
can be explained as follows. For small d1=d2
the peak is very narrow and almost doesn't feel the boundary and thus the escape
time in prone for numerical errors. In fact, for d1=d2
small enough the peak doesn't travel at all or travels to some arbitrary spurious
position in the domain (not necessarily the center of the domain). On the other
hand, the sharp deviation from the strait fit for large d1=d2
is due to the fact that the v component is very spread and it is subject
to large boundary effects. See for example the left-most snapshot of the traveling
peak in figure 1 where the v component
is deformed due to the boundary. This interaction with the boundary has the net
effect of pulling more rapidly the peak towards the boundary, resulting on a downward
deviation of the escape time as a function of d1=d2.
. The deviations from the straight fit (see lines in figure 4)
can be explained as follows. For small d1=d2
the peak is very narrow and almost doesn't feel the boundary and thus the escape
time in prone for numerical errors. In fact, for d1=d2
small enough the peak doesn't travel at all or travels to some arbitrary spurious
position in the domain (not necessarily the center of the domain). On the other
hand, the sharp deviation from the strait fit for large d1=d2
is due to the fact that the v component is very spread and it is subject
to large boundary effects. See for example the left-most snapshot of the traveling
peak in figure 1 where the v component
is deformed due to the boundary. This interaction with the boundary has the net
effect of pulling more rapidly the peak towards the boundary, resulting on a downward
deviation of the escape time as a function of d1=d2.
0.25 cm
0.25 cm



Next: BLOW-UP (May 31, 2000) Up: Chemotaxis: blow up and Previous: Chemotaxis: blow up and
Ricardo Carretero
2000-06-23
![\begin{displaymath}
\begin{array}{rcl}
u_t &=& d_1 \nabla^2 u - \chi \nabla(u\na...
...\ [2.0ex]
v_t &=& d_2 \nabla^2 v - \mu v + \beta u,
\end{array}\end{displaymath}](img1.gif)

