


Next: DIRICHLET vs NEUMANN BC Up: Chemotaxis: blow up and Previous: METASTABILITY (May 9, 2000)
We now turn to the study of blow up. From several references
[] blow-up does not occur in one dimension. Thus let
us take the 2-dimensional equations. Since our moving mesh method
is only designed for one dimension let us simplify the 2-dimensional
model by requiring that the solutions is radially symmetric.
Several points have to be noticed. Only a radially symmetric
profile can be incorporated. The disadvantages from our perspective is that
we won't be able to observe metastability since the peak of the
distribution is going to be centered at the origin (center of
the domain). Thus
there is not going to be any bias towards any point of the boundary
and the peak will stay centered at the origin.
By considering a radially symmetric distribution it is possible to reduce
the chemotactic equations (1) to the following
system in polar coordinates
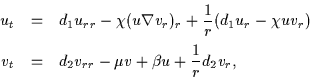 |
(4) |
where the equation for the angle is omitted (radial symmetry) and now the spatial
derivatives are with respect to the radius r. Notice the similarity between
the equations of chemotaxis in one-dimension (2)
and the new equations (4) for the radially
symmetric case. In fact the latter are the same as the former with the extra terms
terms proportional to 1/r. In fact there are this terms that are responsible
for the blow-up since for small r they diverge to 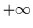 .
.
Figure:
Typical plot of the maximum height of u(r,t)
as a function of t
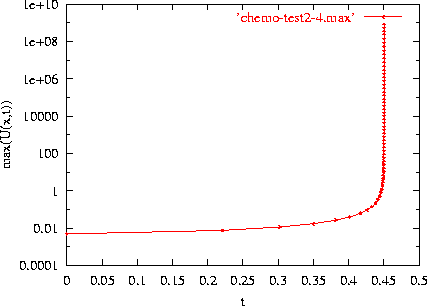 |
The numerical integrations of equations (4)
lead to blow-up in finite time. The first suggestion of blow-up is given in
figure 5 where we depict a typical run for the
behaviour of the maximum of u(x,t) as time evolves. The
figure suggests that the maximum of u blows to infinity (note the logarithmic
scale on the vertical axis) as time approaches a critical time
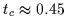 .
.
Figure:
Maximum height of u(r,t) as a function of tc-t.
The fitted line corresponds to
tc=0.450207991,
a = -1.238 and
b = -6.815
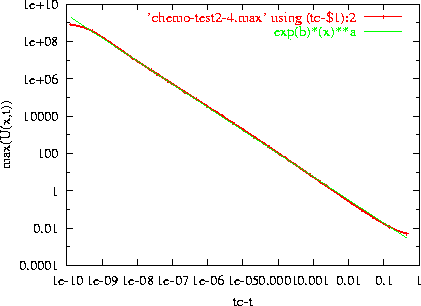 |
The blow-up is made more evident when we plot
max(u(x,t)) as a
function of tc-t in log-log coordinates. The fitted line
shows that the blow up follows closely an expression of the form
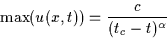 |
(5) |
where c is a constant and 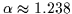 .
.



Next: DIRICHLET vs NEUMANN BC Up: Chemotaxis: blow up and Previous: METASTABILITY (May 9, 2000)
Ricardo Carretero
2000-06-23
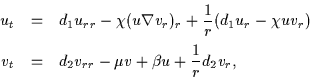
![]() .
.
