DIRICHLET vs NEUMANN BC (Jun 06, 2000)

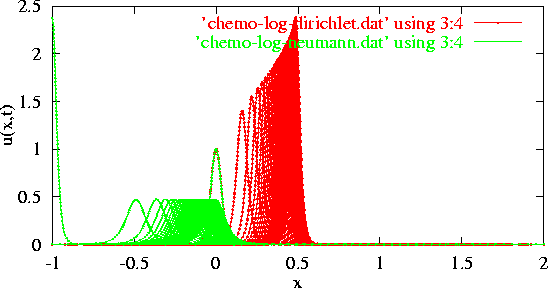
Here we compare numerically the behaviour of the traveling peak for Dirichlet and Neumann boundary conditions. In figure 7 we show the behaviour of u(x,t) as time evolves for Dirichlet (red) and Neumann (green) boundary conditions. For both cases we started with the same initial condition (Gaussian centered at the origin x=0) and the center of the initial condition was chosen not to be at the middle of the domain. As the figure shows, Dirichlet BCs push the peak towards the center of the domain (x=0.5) while Neumann BCs push the peak towards the nearest boundary of the domain (x=-1).

  

Figure: Comparison between Neumann (green) and Dirichlet (red) boundary conditions for traveling peak of the cell concentration.

Maybe it is possible to applied a similar analysis to the one by Ward [2] to have a better understanding of this phenomenon.