Mesh Selection for Moving Frame

The propagation errors in the wavespeed with the fixed frame of reference resulted when the spatial step size $\Delta x$ was too large. For the moving frame of reference, these errors are less significant, but only because smaller step sizes can be taken, e.g., $\Delta x$ is 8 times smaller in the simulation of Figure 2 compared to that of Figure 1.

In fact, the addition of the advection term $\partial \tilde{u}/\partial z$ for moving frame of reference can result in stability problems under spatial discretization if the step size $\Delta x$ is too large. To illustrate this difficulty, consider the moving computational domain $[\underline{z},\overline{z}]=[-25,25]$with only N=10 nodes. The uniformly spaced moving mesh

$$X_j(t) = -25 + \frac{4}{3} t + j\Delta x, \quad j=0,1,\dots,10=N$$

has a step size $\Delta x=5$ which is 4 times larger than for the simulation of Figure 2.

  

Figure: Moving Uniform Mesh $x \in [-25+4t/3,25+4t/3]$, $\Delta x=5$. Exact solution in red. Collocation solution in green with uniformly spaced mesh points in blue.

t=0	t=10	t=20
t=30	t=60	t=90
t=120	t=150	t=180
t=210	t=240	t=270
t=300	t=330	t=360

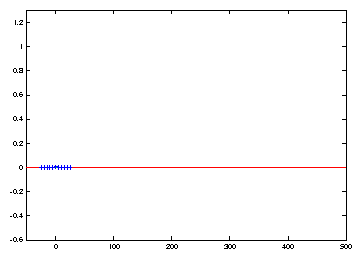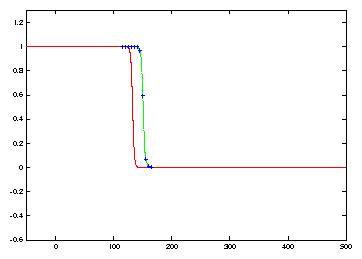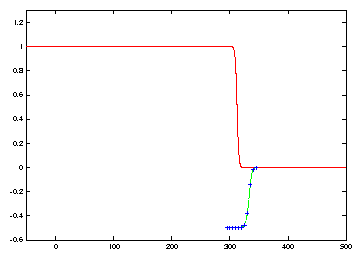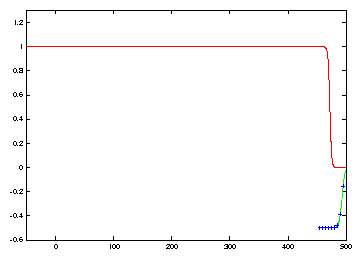
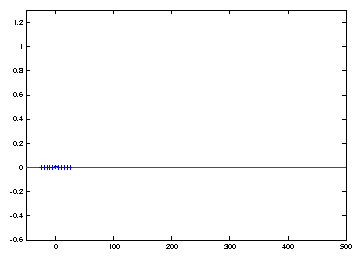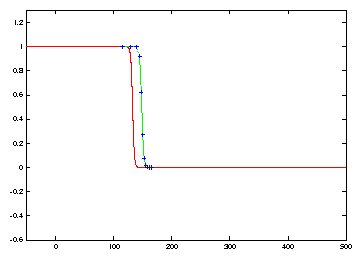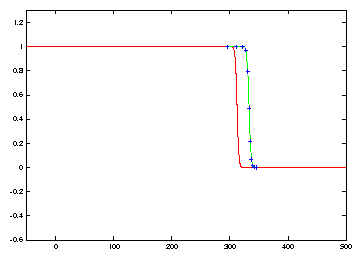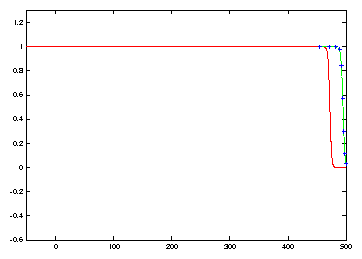
Numerical discretization with method of lines and Hermite collocation leads to oscillatory behaviour near u=0, which can be seen at t=180 in Figure 3. For the case of the Nagumo equation, this oscillation changes the asymptotic behaviour from a monotone decreasing wavefront of speed c₀=4/3to a monotone increasing wavefront of speed c₀=4/3 for $t\ge 240$. This simulation suggests that it is more important to suppress oscillations near unstable equilibria (such as u=0) where even a small perturbation caused by discretization can lead to an entirely different final asymptotic state.

If the method of lines Hermite collocation discretization scheme is applied on a non-uniform mesh where $\Delta x$ is sufficiently small in ``unstable'' regions where $f^{\prime}(u)>0$ then oscillations at the advancing wavefront can be suppressed. Rather than define a non-uniform mesh in advance, we apply the MOVCOL adaptive moving mesh algorithm, and supply a monitor function
$$\begin{align*}M(u,u_{x}) = \sqrt{ \kappa_2 e^{\kappa_1 f^{\prime}(u)} + \biggl[ 25 \frac{\partial u}{\partial x} \biggr]^2} \end{align*}$$
where $\kappa_1, \kappa_2>0$ are weighting parameters to control the mesh spacing. In the following Nagumo simulation, we set $\kappa_1=4.5$ and $\kappa_2=e^{-\kappa_1 f^{\prime}(1)}$so that $\kappa_2 e^{\kappa_1 f^{\prime}(1)}=1$and $\kappa_2 e^{\kappa_1 f^{\prime}(0)}=e^{12},$i.e., the monitor function will place more points in regions where $u \approx 0$ or where $\partial u/\partial x$ is large.

In Figure 4 we see numerical evidence that the oscillations have been suppressed. With only N=10nodes, there is still propagation error, with the discretization moving at a faster speed.

  

Figure: Moving Non-uniform Mesh $x \in [-25+4t/3,25+4t/3]$, N=10. Exact solution in red. Collocation solution in green with non-uniformly spaced mesh points in blue.

t=0	t=10	t=20
t=30	t=60	t=90
t=120	t=150	t=180
t=210	t=240	t=270
t=300	t=330	t=360